Deen Abiola - 24 Dec 2014

Not only are we constantly modeling the world mathematically, animal brains are also constantly proving things about it. The proofs are consistent even if not necessarily sound nor complete. I've not seen it spelled out anywhere before but it's an incredible consequence of the fact that in essence, machine learning is a method to search for programs. For some people this might all read out as obvious and this is a good thing I think. For me, this is a good case study for my philosophy of not keeping things compartmentalized but instead trying to think in terms of bridges from many things to many other things.
In a previous post (Machine Learning is not Magic), I tried to lay the ground for this essay by building some intuitions on learning algorithms; emphasizing them as functions or maps and computations, talking about compression and generalization and identifying causality vs being satisfied with correlations (not in so many words, deserving of its own essay). This essay will serve to more closely link learning with search, logic and computation. It's also worthwhile to spend some time thinking about why machine learning is so desirable: namely because most of the useful things we do are not conscious.
In fact, one of the most interesting things to come out of attempts to build AI is what's known as Moravec's Paradox. Moravec's Paradox is where all the simple stuff we take for granted: vision, speech, walking etc. were expected to be easy while stuff like chess, math, puzzles were thought of as the harder things to implement. Instead it turned out to be the opposite, not just because concepts like common sense are less available and so harder, but because they take a great deal more computational resources while being of higher algorithmic complexity. It's easy to forget how amazingly impressive what virtually every human baby is capable of in a relatively short amount of time; learning the incredibly complex sequences and patterns behind language as well as states of mind they communicate, learning vision, sounds, walking, building a physics model of the world, modeling other humans -- all with minimal guidance (and without being conscious too... mostly...gets in the way?†)!
The bulk of our intelligence is not in our rudimentary puzzle solving abilities; trying to build an AI has taught us that actually, most of the things we thought required minimal intelligence are actually some of the most complex things we do in an objective sense. Moravec also suggested that evolution never got round to optimizing (or there was little benefit for) the deeper logical reasoning computers find easy. This makes sense but I also think there's another more important issue. Reasoning with exact numbers and the extremely large error free scratch spaces computers have requires a great deal of energy while evolution's priority was one of minimizing energy usage above all else. While computers are excellent at forward reasoning/search, humans are (for now) better at pattern matching and recognition since the latter does not require maintaining a massive state space.
There's another consequence of the paradox. It's common to think that in so far that automation is a problem for jobs, more education will fix it. But Moravec's paradox suggests to us that the trade jobs and the jobs requiring the kind of higher order pattern matching that so sets us apart will be safest. It's the management jobs, the rote jobs and entry level jobs across large swathes of industry that will fall. In law, in science, in computing, and yes in manufacture; as long as your job doesn't require constant novel problems difficult to automate, you're a target. This means that it's the graduates, often young, who will be the most affected ones. Fixing the problem will require something more significant than pushing everyone through university.
Suppose I wanted to write a program that could recognize cats or faces or whatever; to write this program would effectively be impossible because a lot of human intelligence is not surfaced. Much of what we do is not made available to us -- it's unconscious -- hence for example, we don't know how it is we tell one person's voice from another's, even with only a very short and distorted listening time. This means that even if there were a simple program behind it, it would not be possible for us to write it.
So what machine learning really is, is auto-programming. Indeed much of how machine learning is currently used -- batch training -- is exactly like scripting in the sense that you run something external to your code that's fixed at development time and hopefully increases flexibility and appearance of intelligence at runtime. In other words, the end products should be considered as little and limited programs and not something magical. But limited in what sense you might ask? Well, the biggest one is that the programs most models learn, even the infamous feed-forward deep learning ones, are not Turing Complete. This is a good thing mostly, it makes search and reasoning about them much easier.
But how do we find these programs automatically? The first thing is to recognize is that the space of programs is mind bogglingly huge; you need some way to quickly guide you to the specific program you're looking for. And the way this is typically done is, paired with some algorithm that uses errors to decide on direction, you feed in lots of data. Data which help divide/categorize the space of examples while also constraining the space of programs to a particular locale. The model which gets output, together with the ML algorithm, specify a program that is able to hopefully accomplish the task we set it to. Barring exceptions like genetic programming -- and also decision trees/forests, I'd argue -- the model itself is not the program. You can't run the model, they're parameters for the algorithm. The algorithm is a function which when run on input data gives us the desired output most of the time. End result is, thanks to machine learning, programs get written tackling tasks which have insufficient conscious availability to have allowed us to have written them ourselves.
It's evident then, but not often remarked upon, that the output of a learning algorithm is (or at least parameters for) a program. This means that learning is a particular kind of search, a search whose end point should be a program that is also a compression of the visited samples, aka generalization. Some people make a distinction between search and optimization but I view this as artificial, serving only to bury opportunities to make connections under trivial details. Optimization might typically only happen on differentiable manifolds -- guided by gradients -- but all that is, is a very specific kind of search, more principled but also more limited (relatively, still huge, basically all state of the art is done in that kind of space) and likely not how the brain implements its specifics.
For something like a Neural Network or Support Vector Machine it's not immediately obvious how training is like searching for a program. Consider a Neural Network, you can think for our purposes, of it as tables of numbers which represent the connections between nodes of a network. Learning involves tweaking those numbers so that when an input vector, a column of data, is fed in, gates (functions like: f (x) = log (1 + exp x)) at each node turn on or not in such a way that input/output pairs similar to those seen in training time are generated. It's a function, a functional program. But how is training like search? What are the parameters?
The output parameters are not the program, instead the parameters tune the model's evaluation algorithm such that it becomes a function specialized to the training data. What I mean by specialization is hard to find a metaphor for and the best I can point to is from computer science itself. The notion of how a general learning algorithm is specialized to a particular function by parameters can be loosely compared to something like the relationship between a regular expression engine and a state machine. The input data specialize and tune the parameters to a program in a similar way that a Levenstein automaton or a depth first automaton might specialize regular expression matching. That's a rough analogy and if it makes no sense then an example based on decision trees might prove clearer.
Decision trees are more obviously programs. They're programs like if x = 3 Or y < 2 then if x = 0 then Car else... etc; they serve to partition the problem space and the search is guided by trying to maximize information gain of each if else split in the data. A bunch of nested if then else statements are more obviously seen as a program and so the search for the best tree is a search, guided by concepts from information theory, for a program which best partitions and explains the observed data. Decision Trees I'd argue, especially because of their interpretability, are closer to how brains represent knowledge (on a conceptual level) than Neural Networks. (Genetic programming is without any ambiguity, a search for programs)
Training a model is exactly a search for a program. One of the most profound concepts in Computer Science is the Curry-Howard Isomorphism. The Curry-Howard Isomorphism links the type systems of computer programs to proofs in logic. The link is not a trivial one, it's rich and deep and has lead to powerful theorem provers but here it suffices to draw the correspondence from types to theorems and programs to proofs (evaluation to implication expansion). What's interesting here is that a machine learning algorithm is an algorithm which searches for programs and programs are proofs hence the act of learning is equivalent to searching for a proof in some non-trivial sense. But proofs of what? It's not clear exactly, since nothing like types are specified. But that doesn't matter since types can be inferred and often, the systems in use are simply typed and decidable. The types are not interesting, being usually very general [e.g. List of< string|number > implies Member of Set{a,b,c}], it's the proofs that are of interest. And since the types are so general, the proofs will not necessarily cover the phenomena even if the theorem is satisfied. But embodied in the programs will be partial proofs on the set of observations being visited.
And as plenty of often cruel experiments have taught us, even things we take for granted†††, like vision and hearing are actually mostly learned. So there's this beautiful observation that in learning to see, every child is learning/searching for a program/building a proof about the behavior of light and objects out in the world. The same is true for hearing, language, walking etc. Not to mention higher order learning. And having learned things, animals end up carrying lots of little programs, evaluating the world and thus carrying out proofs on every observation (e.g. modus ponens) while also, (for the ones that can learn) constantly searching for proofs.
There is a way in which this gets really interesting when applied to Evolution -- not just the program aspect but especially the learning angle. I'll assume for now that the Church Turing Thesis is valid -- not that the universe is a computer but that everything is computing itself. So a rock could be replaced with a Turing Machine that computes a rock as a byproduct or output or whatever without any loss.
Now consider that evolution is a learning algorithm. This is well known and no longer controversial, you can look at it like this: Imagine traits for some population; number of legs, color of fur, height, scale or fur etc. Each organism is placed in an environment. Over time the ones that die will shift the distribution of traits and how this happens is very much like an algorithm computing probability distributions over traits in a way similar to what happens in machine learning (you can link it to Bayesian learning or for sexual evolution, to game playing with weighted majority the manner in which the distribution is balanced/evolved). Mutation is not the main story, it's random and serves mainly to introduce the raw material for evolution. The traits are far less specific of course, corresponding more to genetic units/alleles but the key idea remains.
So we have evolution as search/learning. But what is being learned? I don't know but what is interesting to look at is the driving goal of evolution at all scales: replication. From simple RNA viruses all the way up to humans, replicating close to the current arrangement of atoms is a (the?) major driver.
Then, with evolution as learning and assuming everything can be swapped out without loss with an equivalent Turing machine (or less), then effectively, each organism is the result of a search for a proof related to what it takes to maintain and replicate states in this universe!
But is assuming a Turing machine too strong? Okay, suppose the Church Turing Thesis is wrong. Next, consider that a Turing machine can efficiently simulate, with arbitrary precision, all classical systems. Allow extensions (e.g. quantum Turing machine) and taking into account that everything a Turing machine can do, the universe can as well but the opposite is not true, then: Turing machines are a subset of the universe. So this argument should still hold with the only weakness being if the essence of evolution and cognition require not just incomputable things, but physically unharnessable, no incomputable things only harnessable by brains and the building blocks of living things. This is a very strong assumption and piles on unnecessary complexity, violating Occam's razor.
The common argument, that we used to analogize via clocks etc., is incredibly flawed by taking into account that Clockwork is not universal in the same way a Universal Turing Machine is. Here is what Gödel had to say:
"It may also be shown that a function which is computable ['reckonable'] in one of the systems Si, or even in a system of transfinite type, is already computable [reckonable] in S1. Thus the concept 'computable' ['reckonable'] is in a certain definite sense 'absolute', while practically all other familiar metamathematical concepts (e.g. provable, definable, etc.) depend quite essentially on the system to which they are defined"
† Consciousness
I'm not sure why people put self-consciousness as some kind of pinnacle. I suppose as a seemingly unique human trait, it's placed on a pedestal and worshipped as something that separates us from all other kinds of intelligences. Yet if you look closer, it's not difficult to see that consciousness is very over-rated. 1) As I pointed out above, some of the most incredible feats of intelligence are performed by barely or not even yet conscious human babies. 2) A lot of wisdom, Zen quotes and quotes on mastery are all about shutting down your conscious mind. A novice dancer or martial artist is conscious of all their movements. They're jerky and awkward, where as graceful and fluid movements are only doable once the knowledge has been transferred to the unconscious. This is not just true for automatic movements but for the highest levels of creativity too. 3) The state of flow, where conscious awareness is dimmed and the boundary between self and task is lessened results in the highest levels of performance. 4) People speak often of sleeping on a problem, not thinking about it consciously and having the solution (the brilliant Poincare wrote extensively of this as his method) come to them seeming spontaneously. It seems that all the effortless, graceful and masterful acts are done by the non-conscious part of the brain.
Consciousness is also limited. A large distributed entity would forgo it due to latency and an entity wanting to maintain parallel levels of awareness and threads of cognition will likely think the serial aspect of consciousness too limiting. An entity does not need to be conscious to allow the goals of others to affect which actions it selects nor to model itself against the background of some environment. Consciousness is a tool only; a bookkeeping, blame assigning, goal maintaining tool that's some how morphed into this pointy headed boss that seeks to claim credit for everything that happens in the brain. In fact, I'm having trouble imagining a selfish, jealous, spiteful and petty non-conscious entity.
†† Unreasonable Effectiveness of Mathematics
Assuming the Church Turing Thesis allows all sorts of beautiful links between evolution, learning, logic, proofs and physics to fall out. With compression as generalization we also get links between entropy, Kolmogorov complexity and learning. The physics comes from the link from programs to cartesian closed or monoidal categories. As time goes on, I'm starting to find the Effectiveness of Mathematics not just very reasonable but also, almost...tautological.
††† You can see the experiments on the poor kittens here: Development of the Brain depends on the Visual Environment, https://computervisionblog.wordpress.com/2013/06/01/cats-and-vision-is-vision-acquired-or-innate/.
The wikipedia article on the critical period hypothesis is also worth a look: http://en.wikipedia.org/wiki/Critical_period_hypothesis#Deaf_and_feral_children
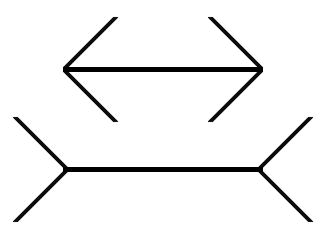
But my favorite example is that the Müller-Lyer illusion is sensitive to whether someone grew up in a city or a desert.
It has been shown that perception of the Müller-Lyer illusion varies across cultures and age groups. Segall, Campbell and Herskovitz[4] compared susceptibility to four different visual illusions in three population samples of Caucasians, twelve of Africans, and one from the Philippines. For the Müller-Lyer illusion, the mean fractional misperception of the length of the line segments varied from 1.4% to 20.3%. The three European-derived samples were the three most susceptible samples, while the San foragers of the Kalahari desert were the least susceptible.