A refrain that I repeat over and over is that many things can be viewed as a prediction game and that better prediction is just better compression. And when someone says something is unpredictable they actually mean this data is highly incompressible - maybe the data generating function is of high kolmogorov complexity or comes from a treacherous search space.
So for example I can tell you that in their core essence, there is not much difference between a scientist and gzip or winzip (actually the best comparison would be 7zip as I explain later). A scientist is trying to make sense of data by creating a simpler description that makes predictions - i.e. compression.
This can be taken literally by doing actual science using something like 7-zip. Using a very simple technique called normalized compression distance - a measure of the similarity between two bit strings by approximating their normalized information distance, itself incomputable since it is based on the Kolmogorov complexity function. For example, one can compare and cluster genomes into phylogenetic trees using 7zip.
To do so I first used the PPMD algo from the 7zip library to compare pairs of files (something like LZW/gzip will not do due to having too small a context though using a larger dictionary cancels this). I then wrote an implementation of the nearest-neighbor chain algorithm for clustering (in F#, no errors, it just worked on first go! Also, in retrospect I see this is easily adaptable to huffman coding).
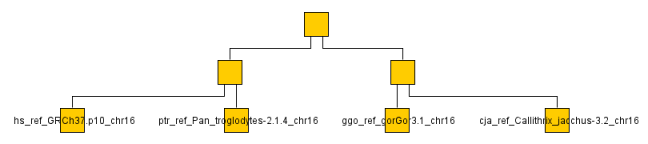
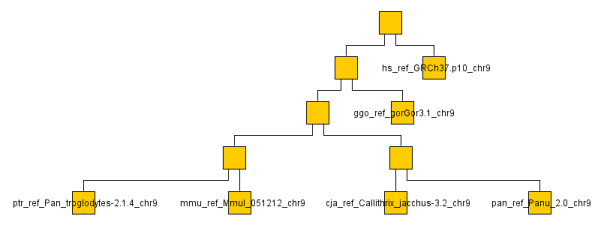
Of course I don't have the time or bandwidth to compare whole genomes so settled for a couple chromosomes across a a handful of monkeys/apes (gorilla, chimp, baboon, rhesus monkey, macaque and human). You can see the resulting graph below even though looking at a single chromosome or two is not very representative. It ran through the O(N^2) algorithm on the ~ 1GB data set in a few minutes on my machine.
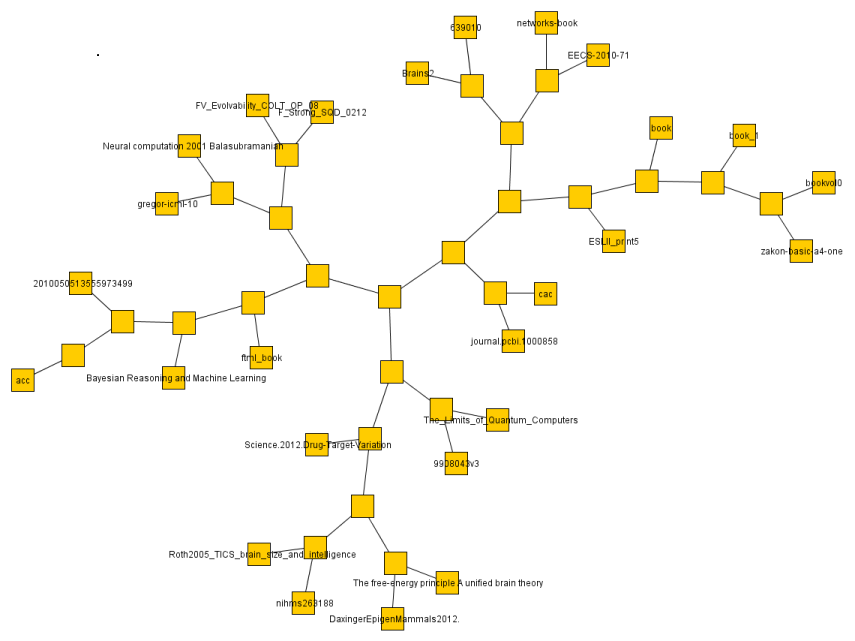
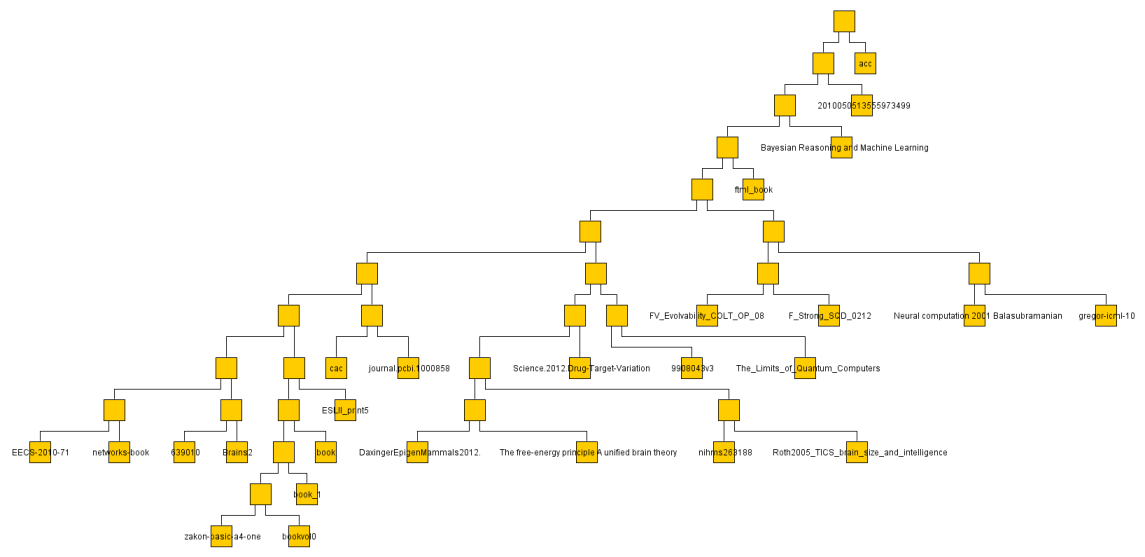
I did the same with some 30 or so text documents (much smaller so faster) and got a result much more easily judged.
Marcus Hutter has an excellent argument for why being able to compress English text at its expected entropy rate ~ 1 bit per character would necessarily signify an AI. In fact top entries in his competition make use of Neural Networks in their compression algorithm and take nearly 10 hours to compress 1GB, blurring the illusory boundaries between Machine Learning and compression. Alas, while impressive they are still mostly limited to the word level. To get better concepts will need to be incorporated.
You can look at it this way. Near perfect compression implies a couple of things. It implies the ability to understand ambiguous contexts, non-specific references and vague language. Such an algorithm would require sophisticated knowledge of not just grammar but knowledge and culture, hence it could read and write English as well as any human.
Consider a simple example of compressing a series of digits such as 14159265... This is at first incompressible but if you recognized it as the decimal portion of pi you could simply represent it symbolically. Of course utilizing all of human knowledge as the model makes a mere look up table and is counter to Occam's Razor. It would be intelligence through brute force stupidity which is not even computationally tractable - hence the need for powerful but smaller models. The more intelligent the model the more it minimizes the data's minimum description length: Length(Model) - log2(probability of data Given Model). We prefer the smaller model not because it is necessarily better but because all things being equal it's much less likely to break way into the future.
I hope after reading this you now have an appreciation for the intelligence behind 7zip (the best open source compression library btw) and how learning, compression, coding and prediction are all related.
The below are the clusters created from the NCDs.


Below is the code. It was not written with optimality in mind although it is still fairly performant (I like that word so nya).
| // Learn more about F# at http://fsharp.net | |
| // See the 'F# Tutorial' project for more help. | |
| open System.IO | |
| open SevenZip | |
| open System | |
| SevenZipCompressor.SetLibraryPath(@"path/to/7z.dll") | |
| let dir = @"files/path/..." | |
| let txts = Directory.GetFiles(dir + @"Test") | |
| let sz = SevenZip.SevenZipCompressor() | |
| let st = System.Diagnostics.Stopwatch() | |
| sz.CompressionMethod <- CompressionMethod.Ppmd | |
| sz.CompressionLevel <- CompressionLevel.Low | |
| let compress2 (f:byte[]) = | |
| use mio = new MemoryStream(f) | |
| use m2 = new MemoryStream(f.Length * 2) | |
| sz.CompressStream(mio, m2) | |
| m2.GetBuffer().[0..int m2.Length - 1] | |
| st.Start() | |
| let compressionMap = txts |> Array.map (fun f -> Path.GetFileNameWithoutExtension f, f |> File.ReadAllBytes |> compress2) |> Map.ofArray | |
| let compredist f1 f2 n1 n2 = | |
| let code = compressionMap.[n1] | |
| let code2 = compressionMap.[n2] | |
| let fxy = Array.append f1 f2 | |
| let code3 = compress2 (fxy) | |
| float(code3.Length - (min (code.Length) (code2.Length))) / float(max (code.Length) (code2.Length)) | |
| let nearEdges = [| for f in txts -> let n1 = Path.GetFileNameWithoutExtension f | |
| n1, | |
| let fbytes = File.ReadAllBytes f | |
| txts |> Array.map (fun fname -> | |
| let n2 = Path.GetFileNameWithoutExtension fname | |
| Path.GetFileNameWithoutExtension fname, compredist fbytes (File.ReadAllBytes(fname)) n1 n2) | |
| |> Array.sortBy snd|] | |
| st.Stop() | |
| let nearEdgesMap = nearEdges |> Map.ofArray | |
| let pairs = nearEdgesMap |> Map.map (fun _ v -> Map.ofArray v) | |
| printfn "%A" nearEdges | |
| type 'a Tree = | |
| | Node of 'a | |
| | Branch of 'a Tree * 'a Tree | |
| type Cluster<'a when 'a : comparison> = | |
| | Singleton of 'a Set | |
| | Clusters of 'a Set * 'a Tree | |
| let completelinkage (ps:Map<'a, Map<'a,float>>) (a: 'a Set) (b:'a Set) = | |
| a |> Set.map (fun item1 -> b |> Set.map (fun item2 -> ps.[item1].[item2]) | |
| |> Set.maxElement) //we only want the two largest pair distances) | |
| |> Set.maxElement | |
| let distclust ps = function | |
| | Singleton (item), Clusters(items, _) -> completelinkage ps item items | |
| | Clusters (items, _) , Singleton(item) -> completelinkage ps items item | |
| | Clusters (items1, _), Clusters(items2, _) -> completelinkage ps items1 items2 | |
| | Singleton (item1) , Singleton(item2) -> ps.[item1.MaximumElement].[item2.MaximumElement] | |
| let mergeClusters = function | |
| | Singleton (item), Clusters(items, dendogram) | |
| | Clusters (items, dendogram) , Singleton(item) -> Clusters(Set.union item items, Branch(dendogram, Node item.MinimumElement)) | |
| | Clusters (items1, dendogram1), Clusters(items2, dendogram2) -> Clusters(Set.union items1 items2, Branch(dendogram1, dendogram2)) | |
| | Singleton (item1) , Singleton(item2) -> Clusters(Set.union item1 item2, Branch(Node item1.MinimumElement, Node item2.MinimumElement)) | |
| let r = Random() | |
| (* | |
| A function that takes a cluster and a set of clusters and finds the nearest item using cluster dist functions | |
| A function that takes a cluster and an item and calculates distance as maxdist (item, clustermember) | |
| There is a map that holds every item and its neighbiors | |
| If we have an item we find the closest item by looking it up in the map. | |
| But we also need to find the closest in the cluster. So we must compare the item to a cluster | |
| To do this we for each cluster, compare the distance to our current item | |
| If an item is closest we add the merged 2 to the cluster stack as a branch and remove the item from actives | |
| If a cluster is closest we merge the item to the tree, remove it from the cluster stack and add the new tree to the stack | |
| If the next item we are looking at is a cluster we must find the closest item. | |
| To find it in the single set we map each item to its distance from the cluster using dist clust | |
| We also sort the cluster set by distance from current cluster | |
| Again if the single item is the closest we merge with cluster and remove from map; | |
| If the cluster is the closest we remove both clusters from clusterset, merge them and put them back | |
| Recurse | |
| Item , Item -> Pack as a Singleton | |
| *) | |
| // (clusterset : Map<string, string Cluster>) | |
| let asCluster x = Singleton (set [x]) | |
| let closestinActives distances cluster (item : string Set) = | |
| item |> Set.map (fun s -> distclust distances (asCluster s, cluster), s) | |
| |> Set.minElement | |
| let find points first closest (distances : Map<string, Map<string,float>>) = | |
| let initialActives = points |> Set.ofArray |> Set.remove first | |
| |> Set.remove closest | |
| let rec seek (stack : string Cluster list) (actives : string Set) = | |
| let current = stack.Head | |
| if stack.Length = 1 && actives = Set.empty then current | |
| else | |
| let nextDist, next = if actives.Count = 0 then Double.MaxValue,"" else closestinActives distances current actives | |
| if stack.Length = 1 then seek (asCluster next :: stack) (actives.Remove(next)) | |
| else let topofstack = stack.Tail.Head | |
| let stackDist = distclust distances (topofstack, current) | |
| if nextDist < stackDist then | |
| seek (asCluster next :: stack) (actives.Remove(next)) | |
| else seek ((mergeClusters (current, topofstack)) :: (stack.Tail.Tail)) actives | |
| seek [asCluster closest ; asCluster first] initialActives | |
| let rec toGraph depth = function | |
| | Node(x) -> x, "", " node\r\n [\r\n id\t\""+x+"\"\r\n label\t\"" + x + "\"\r\n ]\r\n" | |
| | Branch(ltree,rtree) -> let lname, lgraph, names1 = toGraph (depth + 1) ltree | |
| let rname, rgraph, names2 = toGraph (depth + 1) rtree | |
| let name = string (r.Next(0, int(2. ** (float depth + 9.))) ) | |
| name, sprintf "%s\r\n%s\r\n edge\r\n [\r\n source\t\"%s\"\r\n target\t\"%s\"\r\n ]\r\n edge\r\n [\r\n source\t\"%s\"\r\n target\t\"%s\"\r\n ]" | |
| lgraph rgraph name lname name rname, | |
| (sprintf " node\r\n [\r\n id\t\"%s\"\r\n label\t\"\"\r\n ]\r\n" name) + names1 + names2 | |
| let first = fst nearEdges.[r.Next(0,txts.Length)] | |
| let closest = fst nearEdgesMap.[first].[1] | |
| let items, fcluster = (function | Clusters(leset, letree) -> leset, letree) (find (nearEdges |> Array.map fst) first closest pairs) | |
| let _, outgraph, nodes = toGraph 0 fcluster | |
| let n = "graph [" + nodes + outgraph + "]" | |
| File.WriteAllText("mbook.gml", n) | |
lit.er.al.ly adv.
Usage Problem
Usage Note: For more than a hundred years, critics have remarked on the incoherency of using literally in a way that suggests the exact opposite of its primary sense of "in a manner that accords with the literal sense of the words." In 1926, for example, H.W. Fowler cited the example "The 300,000 Unionists ... will be literally thrown to the wolves." The practice does not stem from a change in the meaning of literally itselfif it did, the word would long since have come to mean "virtually" or "figuratively"but from a natural tendency to use the word as a general intensive, as in They had literally no help from the government on the project, where no contrast with the figurative sense of the words is intended.